集群的全局视角¶

OneFlow 提出了 全局视角（Global View） 的概念，用于简化分布式训练。简单而言，在 OneFlow 的全局视角下，集群被抽象为一台“超级计算设备”。

用户不用关心集群中计算、通信的细节，只需关心逻辑上的数据与计算，依然像单机单卡那样思考、编程，就能进行分布式训练。

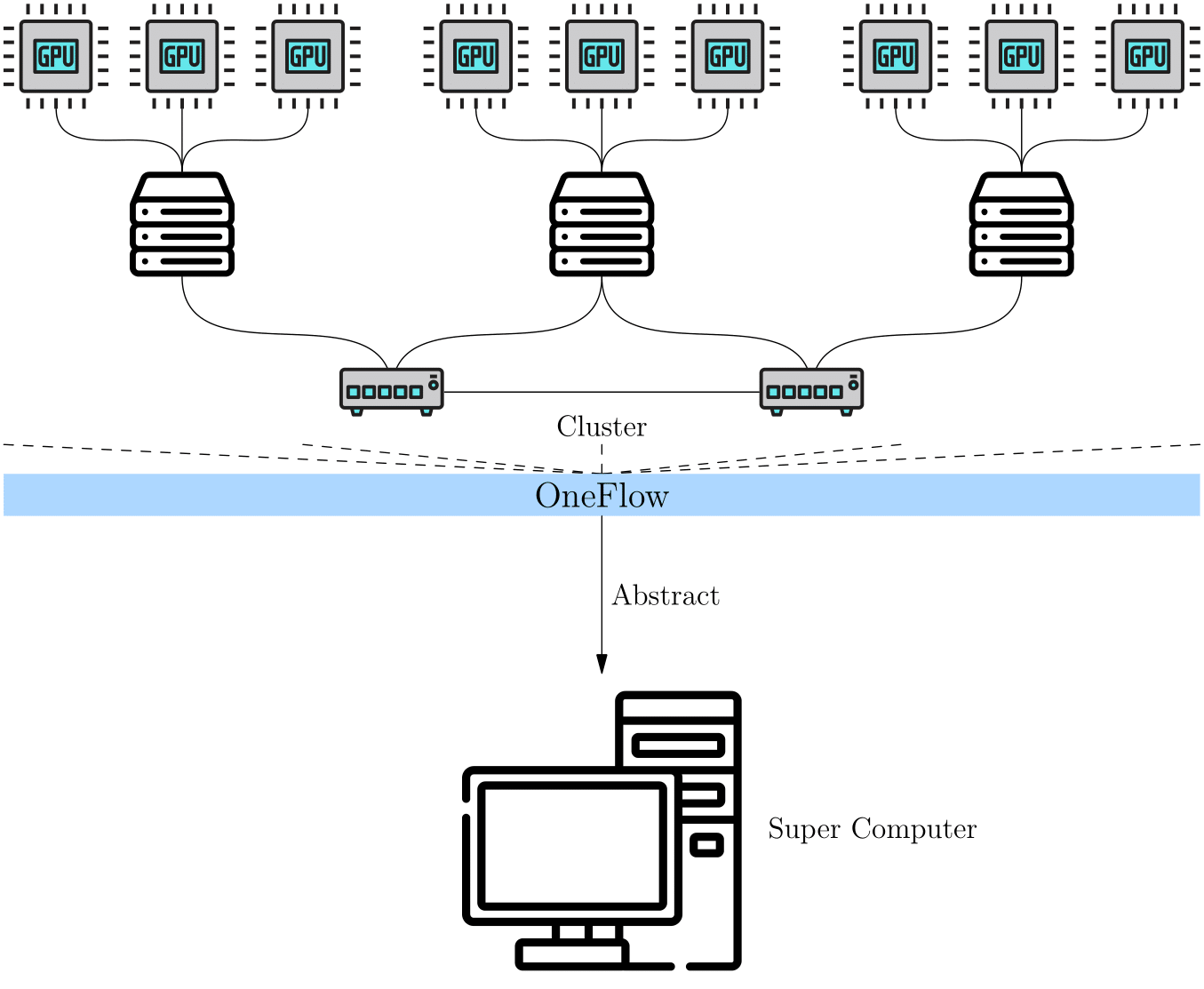
global view

OneFlow 的全局视角，依赖几个重要概念：Placement、SBP 与 SBP Signature。

Placement¶

OneFlow 全局视角下的 Tensor 有 placement 属性，通过 placement 属性可以指定该 Tensor 存放在哪个物理设备上。

OneFlow 会自动为集群中的计算设备编号。比如，如果集群中有 4 台主机，每台主机上有 8 张显卡，一共 32 张显卡，那么 OneFlow 会将这 32 张显卡自动编号为 0~31。

如果想将 Tensor 放置在第 0 台机器的前 4 张显卡上，只需要配置：placement("cuda", [0, 1, 2, 3])。

如果想将 Tensor 放置在第 0 台机器的后 4 张显卡上，只需要配置：placement("cuda", [4, 5, 6, 7])。

placement 使得 OneFlow 很容易支持流水并行，我们将在本专题的其它文章中看到与 placement 有关的实际例子。

SBP¶

SBP 是 OneFlow 发明的概念，描述了“超级计算设备”全局视角下的数据与集群中真实的物理设备上的数据的映射关系，它由 split, broadcast, partial 的首字母组合而成。

详细而言：

split 表示物理设备上的 Tensor，是将全局视角的 Tensor 切分得到的。切分时，需要指定切分的维度。物理设备上的 Tensor ，经过拼接，可以还原得到全局视角的 Tensor 。
broadcast 表示全局视角下的 Tensor，会复制并广播到所有的物理设备上。
partial 表示全局视角下的 Tensor 与物理设备上的 Tensor 的 形状相同，但是物理设备上的值，只是全局视角下 Tensor 的 一部分。以 partial sum 为例，如果我们将集群中所有设备的张量按位置相加，那么就可以还原得到全局视角的 Tensor。除了 sum 外，min、max 等操作也适用于 partial。

下图中分别展示了 SBP 的情况，分别是 split(0)、split(1)、broadcast 和 partial sum。

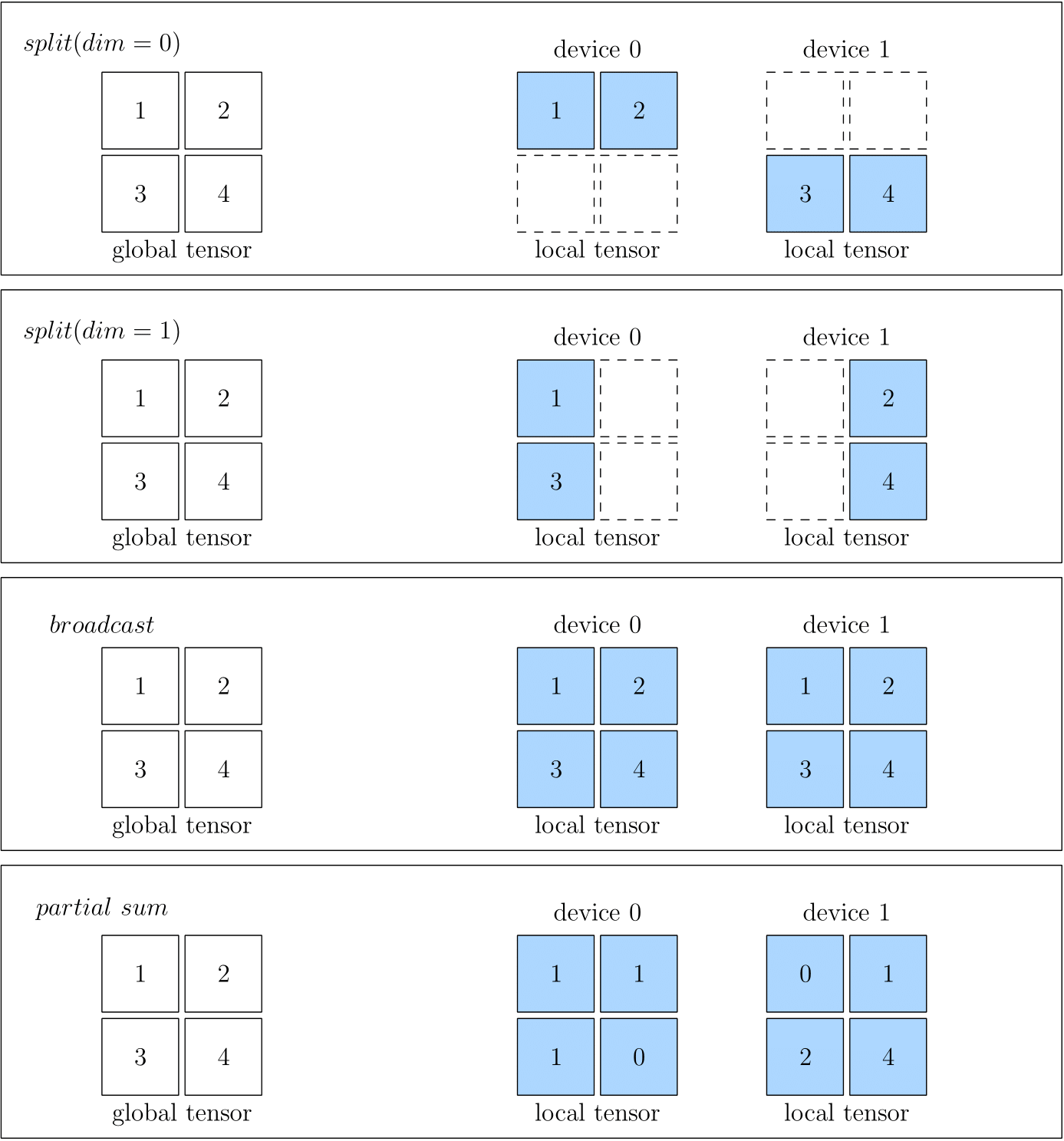
SBP Example

在创建 Global Tensor 时，可以指定 Tensor 的 SBP，实际的代码例子将在下一篇文章 Global Tensor 中看到。

SBP Signature¶

SBP 描述了全局视角下的数据与物理设备上的数据的映射关系，当进行分布式训练时，OneFlow 根据数据的 SBP 属性，将数据分发到各个物理设备，进行计算，并输出结果。

对于一个孤立的 Tensor，我们可以随意设置它的 SBP 属性。但是，对于一个有输入、输出数据的算子，我们却不可以随意设置它的输入、输出的 SBP 属性。这是因为随意设置一个算子输入输出的 SBP 属性，可能不符合全局视角下算子的运算法则。

让我们以矩阵乘法为例讨论这个问题。看看在有2个设备的分布式系统中，矩阵乘法的输入、输出的 SBP 要如何组合才合法，如何组合不合法。

假设全局视角下要，一个形状为 $(m, k)$ 的矩阵 $A$ 与形状为 $(k, n)$ 的矩阵 $B$ 相乘得到 $Y$ ， $Y$ 的形状必然为 $(m, n)$ 。

依据矩阵乘法的规律，我们可以将矩阵 $A$ 按第0维进行切分，切分为形状分别为 $(m_{0}, k)$ 、 $(m_{1}, k)$ 的两个矩阵： $A_{0}$ 和 $A_{1}$ ，然后在2个设备上分别计算：

设备一：

\begin{matrix} A_{0} \times B = Y_{0} \\ (m_{0}, k) (k, n) (m_{0}, n) \end{matrix}

设备二：

\begin{matrix} A_{1} \times B = Y_{1} \\ (m_{1}, k) (k, n) (m_{1}, n) \end{matrix}

我们容易得到物理设备上的 $A_{0}$ 、 $A_{1}$ 与全局视角 $A$ 的关系，以及 $Y_{0}$ 、 $Y_{1}$ 与全局视角数据 $Y$ 的关系：

\begin{matrix} A & = c o n c a t & (A_{0}, & A_{1}) \\ (m, k) & (m_{0}, k) & (m_{1}, k) \end{matrix}

\begin{matrix} Y & = c o n c a t & (Y_{0}, & Y_{1}) \\ (m, n) & (m_{0}, n) & (m_{1}, n) \end{matrix}

注意：以上的 concat 表示拼接操作。

可见，按照以上的方式，将全局视角的数据分发到各个物理设备上，是能够完成运算，并且最终得到全局视角上的正确结果的。以上较长的篇幅，若 使用 SBP 来描述，会变得异常简单 ：

$A$ 为 split(0)， $B$ 为 broadcast，运算结果 $Y$ 为 split(0)。

可见，对于矩阵乘法而言，其输入输出的 SBP，按以上方式组合，是合法的。对于矩阵乘法而言，合法的 SBP 组合不止一种，比如还可以是：

$A$ 为 broadcast， $B$ 为 split(1)，运算结果 $Y$ 为 split(1)。

或者：

$A$ 为 split(1)， $B$ 为 split(0)，运算结果 $Y$ 为 partial sum。

虽然展示了多个合法的 SBP 组合，但是并不是任意的 SBP 组合都是合法的，比如对于矩阵乘法，如果 $A$ 、 $B$ 均为 split(0)，那么：

\begin{matrix} A & = c o n c a t & (A_{0}, & A_{1}) \\ (m, k) & (m_{0}, k) & (m_{1}, k) \end{matrix}

\begin{matrix} B & = c o n c a t & (B_{0}, & B_{1}) \\ (k, n) & (k_{0}, n) & (k_{1}, n) \end{matrix}

那么在物理设备上，因为 $A_{0}$ 与 $B_{0}$ 的形状，并不满足矩阵乘法的要求，也就无法在物理设备上完成矩阵乘法。我们可以说， $A$ 为 split(0)， $B$ 为 split(0) 的 SBP 组合是不合法的。

我们将上文出现的，对于某个算子，其输入输出的一个 特定的、合法的 SBP 组合，称为这个算子的一个 SBP Signature。

SBP Signature 自动推导¶

有了 SBP Signature 的概念后，我们可能会提出几个问题：

用户是否要知道算子的所有 SBP Signature，才能用 OneFlow 做好分布式训练？
作为算法工程师，用户是否要为每层网络都设置输入的 SBP？

对于前一个问题，用户当然不需要知晓算子所有的 SBP Signature。罗列某个算子所有可能的 SBP Signature 的工作，是 算子作者 的责任。算子作者根据算子的运算法则，在开发算子时，就已经罗列并预设好该算子所有可能的 SBP Signature。

这顺便就解答了第二个问题：因为有预设好的 SBP Signature，所以，某一层算子只要有输入的 SBP，OneFlow 就可以根据 SBP Signature 推导出该层算子输出的 SBP。而上游算子的输出，又是下游算子的输入，这样，就确定了下游算子输入的 SBP，然后又可以根据 SBP Signature 确定更下游输出的 SBP…… 这样不断推导、传播。因此通常情况下，用户是不需要为每层网络都设置输入的 SBP。而只有最初输入层，或者需要强制指定某层的 SBP 时，才需要显式指定。

用户还可能会有新的问题：

一个算子的合法 SBP Signature 常常有多个，OneFlow 运行时到底会选择哪一个呢，它是依据什么做出选择的？

对于这个问题，需要了解 OneFlow 的 SBP Signature 自动推导 机制。所谓的 SBP Signature 自动推导，指的是：在给定所有算子的所有合法的 SBP Signature 的前提下，OneFlow 有一套算法，会基于传输代价为每种合法的 SBP Signature 进行打分，并选择传输代价最小的那个 SBP Signature。这样使得系统的吞吐效率最高。

Boxing 机制¶

严格地说，OneFlow 的 Boxing 机制对于用户其实是透明的，用户使用 OneFlow 做分布式训练时，不用知晓它也感知不到它。

但是，鉴于某些深入思考的用户，可能了解 SBP Signature 自动推导后，会自然提出以下问题：

如果 OneFlow 自动选择的 SBP Signature，上一层算子的输出与下一层算子的输入的 SBP 属性不匹配时，那怎么办呢？

举个具体例子，比如以下代码中，上一层算子 matmul 的输出 SBP 本来是 split(0)，但是下一层算子 matmul 的输入，被转成了 broadcast。此时，上一层的输出与下一层的输入，它们的 SBP 其实就不一致了。

import oneflow as flow

P0 = flow.placement("cuda", ranks=[0, 1])
P1 = flow.placement("cuda", ranks=[2, 3])
a0_sbp = flow.sbp.split(0)
b0_sbp = flow.sbp.broadcast
y0_sbp = flow.sbp.broadcast
b1_sbp = flow.sbp.split(1)

A0 = flow.randn(4, 5, placement=P0, sbp=a0_sbp)
B0 = flow.randn(5, 8, placement=P0, sbp=b0_sbp)
Y0 = flow.matmul(A0, B0)

Y0 = Y0.to_global(placement=P1, sbp=y0_sbp)
B1 = flow.randn(8, 6, placement=P1, sbp=b1_sbp)
Y2 = flow.matmul(Y0, B1)

这种情况下，OneFlow 其实会检测到这种不一致，并且在上游的输出和下游的输入间插入一个算子，做相关的转换工作。这类自动加入做转换的算子，就称为 Boxing 算子。

以上代码的逻辑图和物理执行图的对应关系如下：

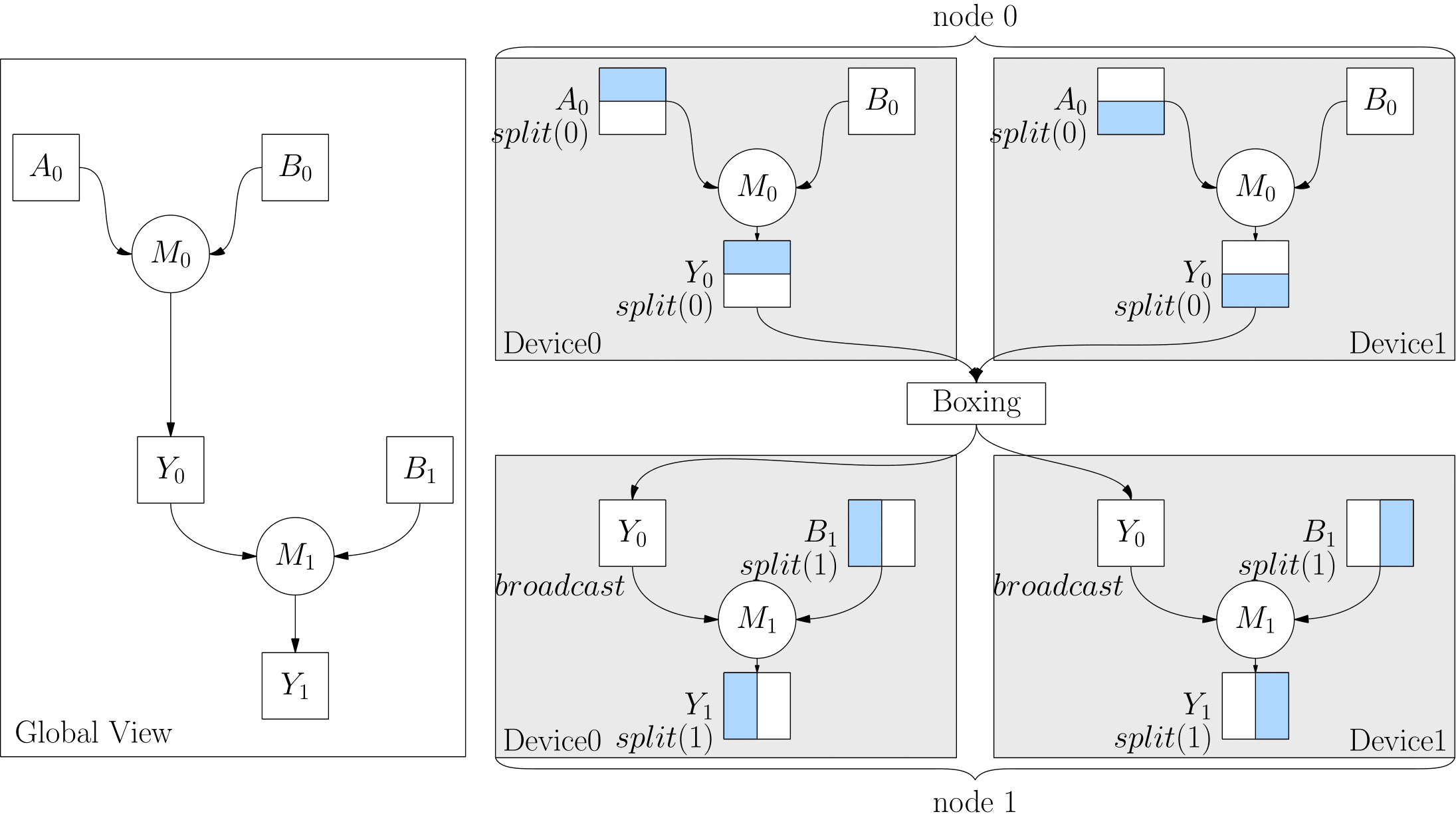
总结¶

placement 与 SBP、SBP Signature 是 OneFlow 分布式全局视角的重要保证，OneFlow 的全局视角使得 OneFlow 的分布式训练与单机单卡一样简单。

通常情况下，用户只需要在起始网络层设置 SBP，由此可以省略传统分布式训练中手写通信操作的麻烦。更值得一提的是，除了本文介绍的 SBP Signature 自动推导机制外，OneFlow 团队正在研发一种寻求全局最优解的自动并行方法，正在内测，等它上线后，用户可以不做任何 SBP 配置就得到很好的分布式训练效果，敬请期待。

在下一篇 Global Tensor 中，我们将看到全局视角的编程例子。