Autograd¶
神经网络的训练过程离不开 反向传播算法,在反向传播过程中,需要获取 loss 函数对模型参数的梯度,用于更新参数。
OneFlow 提供了自动求导机制,可自动计算神经网络中参数的梯度。
本文将先介绍计算图的基本概念,它有利于理解 OneFlow 自动求导的常见设置及限制,再介绍 OneFlow 中与自动求导有关的常见接口。
计算图¶
张量与算子,共同组成计算图,如以下代码:
import oneflow as flow
def loss(y_pred, y):
return flow.sum(1/2*(y_pred-y)**2)
x = flow.ones(1, 5) # 输入
w = flow.randn(5, 3, requires_grad=True)
b = flow.randn(1, 3, requires_grad=True)
z = flow.matmul(x, w) + b
y = flow.zeros(1, 3) # label
l = loss(z,y)
它对应的计算图如下:
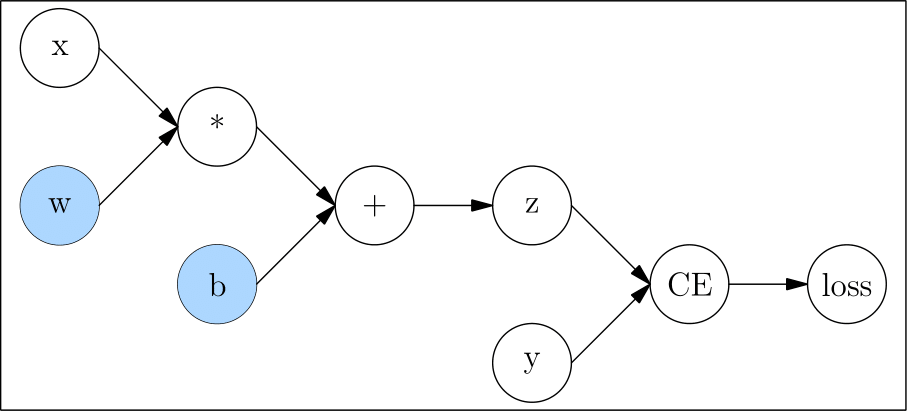
计算图中,像 x、w、b、y 这种只有输出,没有输入的节点称为 叶子节点;像 loss 这种只有输入没有输出的节点,称为 根节点。
反向传播过程中,需要求得 l 对 w、b 的梯度,以更新这两个模型参数。因此,我们在创建它们时,设置 requires_grad 为 True。
自动求梯度¶
backward 与梯度¶
在反向传播的过程中,需要得到 l 分别对 w、b 的梯度 \(\frac{\partial l}{\partial w}\) 和 \(\frac{\partial l}{\partial b}\)。我们只需要对 l 调用 backward() 方法,然后 OneFlow 就会自动计算梯度,并且存放到 w 与 b 的 grad 成员中。
l.backward()
print(w.grad)
print(b.grad)
tensor([[0.9397, 2.5428, 2.5377],
[0.9397, 2.5428, 2.5377],
[0.9397, 2.5428, 2.5377],
[0.9397, 2.5428, 2.5377],
[0.9397, 2.5428, 2.5377]], dtype=oneflow.float32)
tensor([[0.9397, 2.5428, 2.5377]], dtype=oneflow.float32)
对非叶子节点求梯度¶
默认情况下,只有 requires_grad=True 的叶子节点的梯度会被保留。非叶子节点的 grad 属性默认在 backward 执行过程中,会自动释放,不能查看。
如果想保留并查看非叶子节点的梯度,可以调用 Tensor.retain_grad 方法:
from math import pi
n1 = flow.tensor(pi/2, requires_grad=True)
n2 = flow.sin(n1)
n2.retain_grad()
n3 = flow.pow(n2, 2)
n3.backward()
print(n1.grad)
print(n2.grad)
以上代码,既求 \(\frac{\partial n_3}{\partial n_1}\),也求 \(\frac{\partial n_3}{\partial n_2}\)
输出:
tensor(-8.7423e-08, dtype=oneflow.float32)
tensor(2., dtype=oneflow.float32)
对一个计算图多次 backward()¶
默认情况下,对于给定的计算图,只能调用 backward() 一次。比如,以下代码会报错:
n1 = flow.tensor(10., requires_grad=True)
n2 = flow.pow(n1, 2)
n2.backward()
n2.backward()
报错信息:
Maybe you try to backward through the node a second time. Specify retain_graph=True when calling .backward() or autograd.grad() the first time.
如果想要在同一个计算图上调用多次 backward(),需要在调用时设置 retain_graph=True。
n1 = flow.tensor(10., requires_grad=True)
n2 = flow.pow(n1, 2)
n2.backward(retain_graph=True)
print(n1.grad)
n2.backward()
print(n1.grad)
输出:
tensor(20., dtype=oneflow.float32)
tensor(40., dtype=oneflow.float32)
以上输出可知,OneFlow 会 累加 多次 backward() 计算得到的梯度。
如果想清空梯度,可以调用 zeros_ 方法:
n1 = flow.tensor(10., requires_grad=True)
n2 = flow.pow(n1, 2)
n2.backward(retain_graph=True)
print(n1.grad)
n1.grad.zeros_()
n2.backward()
print(n1.grad)
输出:
tensor(20., dtype=oneflow.float32)
tensor(20., dtype=oneflow.float32)
不记录某个 Tensor 的梯度¶
默认情况下,OneFlow 会 tracing requires_grad 为 True 的 Tensor,自动求梯度。
不过有些情况可能并不需要 OneFlow 这样做,比如只是想试一试前向推理。那么可以使用 oneflow.no_grad 或 oneflow.Tensor.detach 方法设置。
z = flow.matmul(x, w)+b
print(z.requires_grad)
with flow.no_grad():
z = flow.matmul(x, w)+b
print(z.requires_grad)
输出:
True
False
z_det = z.detach()
print(z_det.requires_grad)
输出:
False
输出不是标量时如何求梯度¶
通常,调用 backward() 方法的是神经网络的 loss,是一个标量。
但是,如果不是标量,对 Tensor 调用 backward() 时会报错。
x = flow.randn(1, 2, requires_grad=True)
y = 3*x + 1
y.backward()
报错信息:
Check failed: IsScalarTensor(*outputs.at(i)) Grad can be implicitly created only for scalar outputs
而对 y 求 sum 后可以求梯度:
x = flow.randn(1, 2, requires_grad=True)
y = 3*x + 1
y = y.sum()
y.backward()
print(x.grad)
输出:
tensor([[3., 3.]], dtype=oneflow.float32)
错误原因及解决方法的分析请参考下文 “扩展阅读” 部分。
扩展阅读¶
x 张量中有两个元素,记作 \(x_1\) 与 \(x_2\),y 张量中的两个元素记作 \(y_1\) 与 \(y_2\),并且两者的关系是:
此时,想直接求 \(\frac{\partial \mathbf{y}}{\partial \mathbf{x}}\)
在数学上是没有意义的,因此当然就报错了。
实际上,当用户调用 y.backward() 时,其实想要的结果通常是:
当对 y 进行 sum 运算后:
此时,调用 backward() 时,对 \(x_1\) 和 \(x_2\) 可求梯度:
除了使用 sum 之外,还可以使用更通用方法,即 Vector Jacobian Product(VJP) 完成非标量的根节点的梯度计算。依然用上文的例子,在反向传播过程中,OneFlow 会根据计算图生成雅可比矩阵:
只需提供一个与 \(\mathbf{y}\) 大小一致的向量 \(\mathbf{v}\),即可计算 VJP:
若向量 \(\mathbf{v}\) 是反向传播中上一层的梯度,VJP 的结果刚好是当前层要求的梯度。
backward 方法是可以接受一个张量做参数的,该参数就是 VJP 中的 \(\mathbf{v}\),理解以上道理后,还可以使用以下的方式对张量求梯度:
x = flow.randn(1, 2, requires_grad=True)
y = 3*x + 1
y.backward(flow.ones_like(y))
print(x.grad)
输出:
tensor([[3., 3.]], dtype=oneflow.float32)
外部链接